Related Work on Inextensible Surface Reconstruction

A popular assumption made in deformable surface reconstruction is to consider that the surface to reconstruct is inextensible (164,144,176,166). This assumption is reasonable for many types of material such as paper and some types of fabrics. Having an inextensible surface means that the surface is an isometric deformation of the reference shape. Another way of putting it is to say that the length of the geodesics between pairs of points remains unchanged when the surface deforms. An exact transcription of this principle is difficult to integrate in a reconstruction algorithm. Indeed, while it is trivial to compute the geodesic in a flat reference shape, it is quite difficult to do it for a bent surface (especially when the surface is represented as a sparse set of points or a triangular mesh). Many approximations have thus been proposed.

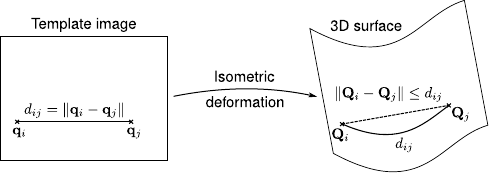
The first type of approximation consists in saying that if the surface does not deform too much then the Euclidean distance is a good approximation to the geodesic distance. Such an approach has been used for instance in (202,164,176,163). Note that these types of constraints are usually set in a soft way. For a given set of point pairs on the surface, the Euclidean distance should not diverge too much from the geodesic distances. This approximation is better when there are a large number of points. Depending on the surface model it is not always possible to vary the number of points.

Although the Euclidean approximation can work well in some cases, this approximation gives poor results when creases appear in the 3D surface. In this case, the Euclidean distance between two points on the surface can shrink, as illustrated in figure 7.1.

Figure 7.1: Inextensible object deformation. The Euclidean distance between two points is necessarily less than or equal to the length of the geodesic that links those two points (this length is easily computable if we have a template image representing the flat reference surface from a fronto-parallel point of view).

The `upper bound approach' is a now classical approach (144,166) which consists in noticing that even if the Euclidean distance between two points can shrink it can never be greater than the length of the corresponding geodesic. In other words, the inextensibility constraint  $\Vert \mathbf{Q}_i - \mathbf{Q}_j \Vert \leq d_{ij}$ must be satisfied for any pair of points $(\mathbf{Q}_i, \mathbf{Q}_j)$ lying on the surface. The second principle of such algorithms is to say that a 3D point  $\mathbf{Q}_i$ must lie on the sightline  $\mathbf{u}_i$, i.e. $\mathbf{Q}_i = \mu_i \mathbf{u}_i$. These two constraints are not sufficient to reconstruct the surface. Indeed, nothing prevents the reconstructed surface from shrinking towards the optical centre of the camera. This problem is `solved' using a heuristic that has been proven to be very effective in practice. It consists in considering a perspective camera and in maximizing the depth of the reconstructed 3D points.

These ideas have been implemented in different manners. For instance, (144) proposes a dedicated algorithm that enforces the inextensibility constraints. This algorithm accounts for noise only in the template image (by simply increasing a little bit the geodesic distances in the template, i.e. by replacing $d_{ij}$ with $d_{ij} + \varepsilon_{\mathcal {T}}$ where  $\varepsilon_{\mathcal {T}}$ is the maximal inaccuracy of the points in the template image). Another sort of implementation is given by (164,166). In these papers, a convex cost function combining the depth of the reconstructed points and the negative of the reprojection error is maximized while enforcing the inequality constraints arising from the surface inextensibility. The resulting formulation can be easily turned into an SOCP problem. A similar approach is explored in (176). These last two methods account for noise in the input image. The approach of (144) is a point-wise method. The approaches of (164,176,166) use a triangular mesh as surface model, and the inextensibility constraints are applied to the vertices of the mesh.