Next: Feature-Driven Registration Up: Feature-Driven Direct Non-Rigid Image Previous: Introduction Contents
The registration of images of deformable surfaces has received a growing attention over the past decade. Usually, for purely twodimensional registration, as is the case in this paper, smoothness constraints are used to filter out the noise and `fill-in' the optical flow in untextured image areas. These soft constraints are either implicitly incorporated in a parameterized warp or enforced through regularization. In this paper, we focus on direct as opposed to feature-based methods, e.g. (185,145). In the feature-based methods, the warp parameters are estimated from features, such as points, which have first been extracted and matched in the images to register (181). Note that there exist methods that mix both the feature-based and the direct approaches to image registration. See for instance, (102,81).
Direct registration consists in minimizing the pixel value discrepancy.
Registration of an image sequence is posed as a set of nonlinear optimization problems, each of which estimating
![]() using the registration
using the registration
![]() of the previous frame as an initial solution.
The discrepancy function
of the previous frame as an initial solution.
The discrepancy function
![]() is usually chosen as the two-norm of the difference
is usually chosen as the two-norm of the difference
![]() between the texture image and the current one, warped towards the texture image, i.e.
between the texture image and the current one, warped towards the texture image, i.e.
![]() , giving:
, giving:
Several algorithms have been proposed to minimize
![]() .
We classify them in two groups: the Forward Additive algorithms and the Inverse Compositional ones.
.
We classify them in two groups: the Forward Additive algorithms and the Inverse Compositional ones.
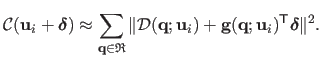 |
(A.2) |
| (A.3) |
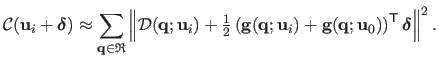 |
(A.4) |
The major drawback of the two above-presented methods is that the image gradient vector for each pixel in
![]() must be recomputed at each iteration.
This is the most expensive step of the process.
A major improvement was proposed by (9) with the Inverse Compositional algorithm.
The first key idea consists in switching the roles of the texture and of the current images:
must be recomputed at each iteration.
This is the most expensive step of the process.
A major improvement was proposed by (9) with the Inverse Compositional algorithm.
The first key idea consists in switching the roles of the texture and of the current images:
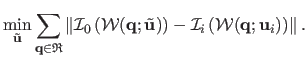 |
(A.5) |
| (A.6) |
As proposed in (158,75,123), these attempts usually consist in finding the best approximating warp for the pixels of interest in
![]() :
:
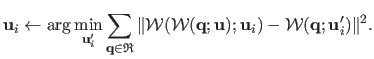 |
(A.7) |
Other methods have been proposed to obviate the shortcomings induced by non-groupwise warps. For instance, one may force the solution space to contain diffeomorphic warps (47,103,102). The solution space thus constitutes a group. Requiring the warps to be diffeomorphisms may be an overly strong requirement. This is especially true when the deformations are not too important. Indeed, as noted in (102), with such deformations the estimated warps may be diffeomorphisms even though the solution space contains non-diffeomorphic warps. Besides, such approaches make the use of standard deformation models such as the TPS and the FFD generally impossible. This is one interesting point of the proposed approach in this paper: it proposes an efficient method which is built on top of the most common deformation models for image registration. Finally, enforcing the estimated warps to be diffeomorphisms is often achieved by adding supplementary constraints to an initial forward estimation algorithm. These constraints are generally impractical to design a fast inverse-compositional estimation algorithm.