Next: Problem Statement and Previous Up: Feature-Driven Direct Non-Rigid Image Previous: Feature-Driven Direct Non-Rigid Image Contents
Registering images of a deforming surface is important for tasks such as video augmentation by texture editing, deformation capture and non-rigid Structure-from-Motion. This is a difficult problem since the appearance of imaged surfaces varies due to several phenomena such as camera pose, surface deformation, lighting and motion blur. Recovering a 3D surface, its deformations and the camera pose from a monocular video sequence is intrinsically ill-posed. While prior information can be used to disambiguate the problem, see e.g. (29,75,145), it is common to avoid a full 3D model by using image-based deformation models, e.g. (16,24,49,111). The Thin-Plate Spline warps (TPS) is one possible deformation model, proposed in a seminal paper by (24), that has been shown to effectively model a wide variety of image deformations in different contexts. Recent work shows that the TPS warp can be estimated not only with the traditional landmark based method, but also with direct methods, i.e. by minimizing the intensity discrepancy between registered images (16,111). Other non-rigid warps include Radial Basis Functions (with e.g. multiquadrics (113) or Wendland's (72) as kernel function) and Free-Form Deformations (162).
The Gauss-Newton algorithm with additive update of the parameters is usually used for conducting the minimization. Its main drawback is that the Hessian matrix must be recomputed and inverted at each iteration. More efficient solutions have been proposed by (9) based on compositional updating of the parameters. They might lead to a constant Hessian matrix. Most non-rigid warps do not form groups, preventing the use of compositional algorithms which require one to compose and possibly invert the warps. Despite several attempts to relax the groupwise assumption by various approximations (158,75,123), there is no simple solution in the literature.
This paper is an extended version of an earlier conference version (76). With respect to the literature, it brings several contributions:
We experimentally show that Feature-Driven algorithms are clearly more efficient without loss of accuracy compared to previous state-of-the-art methods. The combination of the Feature-Driven framework with Learning-based local registration outperforms other algorithms for most experimental setups.
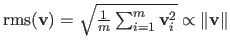 , with
, with
Images are considered as
![]() functionsA.2 and are denoted using calligraphic fonts (
functionsA.2 and are denoted using calligraphic fonts (
![]() ).
If
).
If
![]() is a collection of pixels then
is a collection of pixels then
![]() is the vector in which are stacked the values of
is the vector in which are stacked the values of
![]() for all the pixels indicated in
for all the pixels indicated in
![]() .
More precisely, if
.
More precisely, if
![]() then
then
![]() where
where
![]() is the cardinal of the set
is the cardinal of the set
![]() .
.
The images to be registered are written
![]() with
with
![]() .
The texture image, e.g. the region of interest in the first image, is denoted
.
The texture image, e.g. the region of interest in the first image, is denoted
![]() .
The set of pixels of interest, i.e. the subset of pixels of the image
.
The set of pixels of interest, i.e. the subset of pixels of the image
![]() actually used to estimate a warp, is denoted
actually used to estimate a warp, is denoted
![]() .
A generic parametric warp is written
.
A generic parametric warp is written
![]() .
It depends on a parameter vector
.
It depends on a parameter vector
![]() for image
for image
![]() and maps a point
and maps a point
![]() from the texture image to the corresponding point
from the texture image to the corresponding point
![]() in the
in the ![]() -th image:
-th image:
![]() .
The notation
.
The notation
![]() designates the warp as a function of its parameters, i.e. an
designates the warp as a function of its parameters, i.e. an
![]() function where
function where ![]() is the size of the parameter vector, instead of as a function of the pixels.
is the size of the parameter vector, instead of as a function of the pixels.