Subsections
Feature-Driven Registration
In this section, we present our principal contribution: the Feature-Driven framework.
This framework, in which one directly acts on warp driving features, has two main advantages.
First, it often is better balanced to tune feature positions, expressed in pixels, than coefficient vectors that may be difficult to interpret, as for the TPS or the FFD warps.
Second, it allows one to use the efficient compositional framework in a straightforward manner.
Indeed, warp composition and inversion cannot be directly done for non-groupwise warps.
We propose empirical means for approximating warp composition and inversion through their driving features, called threading and reversion respectively.
Our Feature-Driven framework is generic in the sense that it can be applied to almost any parametric warps such as the TPS or the FFD warps, as shown in section A.5.
Feature-Driven Warp Parameterization
Ignoring the set of parameters, a warp is an
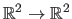 function usually parameterized by a set of
function usually parameterized by a set of 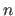 control points
control points
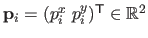 for
for
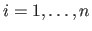 .
These control points are grouped in a vector
.
These control points are grouped in a vector
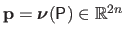 where
where
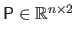 is the matrix defined by
is the matrix defined by
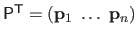 .
We write
.
We write 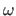 the warp in its natural parameterization.
The warp
the warp in its natural parameterization.
The warp 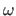 is said to be linear when it can be defined as a linear combination of its control points:
is said to be linear when it can be defined as a linear combination of its control points:
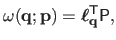 |
(A.8) |
where
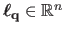 is a vector that depends on the point
is a vector that depends on the point
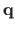 and on the type of warp being considered.
Note that the dependency on
and on the type of warp being considered.
Note that the dependency on
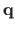 of
of
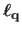 is usually non linear even if the warp is linear.
The control points are usually not interpolated.
They just act as `attractors' to the warp.
It thus makes their interpretation difficult.
The Feature-Driven concept is in fact a change of parameterization.
The control points are replaced by a set of features that are interpolated by the warp.
We call them the driving features and denote them
is usually non linear even if the warp is linear.
The control points are usually not interpolated.
They just act as `attractors' to the warp.
It thus makes their interpretation difficult.
The Feature-Driven concept is in fact a change of parameterization.
The control points are replaced by a set of features that are interpolated by the warp.
We call them the driving features and denote them
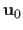 in the texture image and
in the texture image and
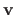 in the current one (see figure A.1).
We denote
in the current one (see figure A.1).
We denote
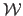 the Feature-Driven parameterization of the warp
the Feature-Driven parameterization of the warp 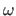 .
Loosely speaking, matching the driving features between two images is equivalent to defining a warp since the warp can be used to transfer the driving features from one image to the other, while conversely, the warp can be computed from the driving features.
Indeed, if the warp is linear with respect to its control points then it is always possible to find a matrix
.
Loosely speaking, matching the driving features between two images is equivalent to defining a warp since the warp can be used to transfer the driving features from one image to the other, while conversely, the warp can be computed from the driving features.
Indeed, if the warp is linear with respect to its control points then it is always possible to find a matrix
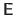 such that:
such that:
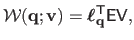 |
(A.9) |
with
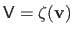 , i.e.
, i.e.
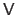 equals to
equals to
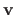 reshaped on two columns.
Matrix
reshaped on two columns.
Matrix
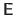 can be pre-computed.
Details on how the matrix
can be pre-computed.
Details on how the matrix
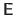 is obtained for the TPS and the FFD warps are given in section A.5.1 and section A.5.2 respectively.
If we write
is obtained for the TPS and the FFD warps are given in section A.5.1 and section A.5.2 respectively.
If we write
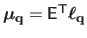 then the Feature-Driven parameterization of the warp
then the Feature-Driven parameterization of the warp
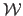 is given by:
is given by:
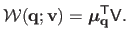 |
(A.10) |
If we denote
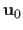 the features in the texture image then
the features in the texture image then
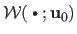 is the identity warpA.3, i.e. the warp that leaves the location of the features
is the identity warpA.3, i.e. the warp that leaves the location of the features
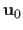 unchanged.
unchanged.
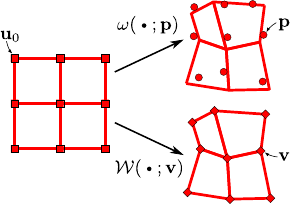
Given two sets of driving features,
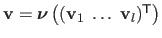 and
and
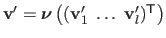 , we want to find a third set
, we want to find a third set
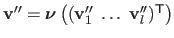 defined such that threading the warps induced by
defined such that threading the warps induced by
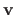 and
and
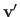 results in the warp induced by
results in the warp induced by
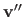 , as shown in figure A.2.
We propose a simple and computationally cheap way to do it, as opposed to previous work.
This is possible thanks to the Feature-Driven parameterization.
Our idea for threading warps is very simple: we apply the
, as shown in figure A.2.
We propose a simple and computationally cheap way to do it, as opposed to previous work.
This is possible thanks to the Feature-Driven parameterization.
Our idea for threading warps is very simple: we apply the
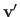 induced warp to the features
induced warp to the features
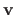 ; the resulting set of features is
; the resulting set of features is
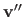 .
We thus define the warp threading operator, denoted
.
We thus define the warp threading operator, denoted
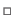 , as:
, as:
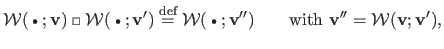 |
(A.11) |
where
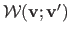 is meant to be applied to each feature in
is meant to be applied to each feature in
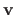 .
.
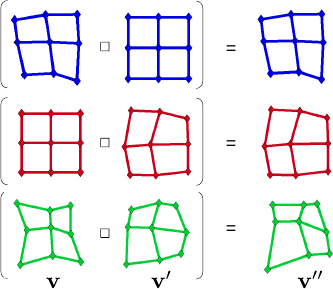
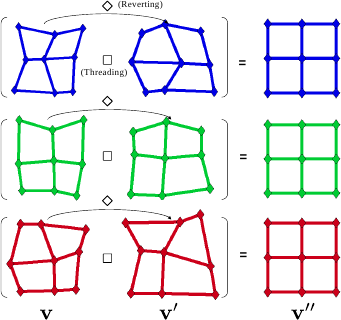
Examples of our warp threading process are shown in figure A.3.
We synthesized two sets of driving features
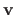 and
and
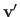 by randomly disturbing a
by randomly disturbing a
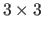 regular grid from its rest position
regular grid from its rest position
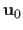 .
As expected, threading a warp
.
As expected, threading a warp
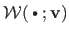 with the identity
with the identity
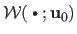 returns the original warp i.e.
returns the original warp i.e.
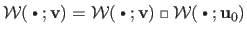 and
and
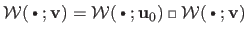 .
.
Figure A.3:
Examples for the warp threading process.
|
 |
Reverting Warps
Given a set
 of driving features, we want to determine the features
of driving features, we want to determine the features
 such that the warp they induce is the reversion of the one induced by
such that the warp they induce is the reversion of the one induced by
 .
This is illustrated in figure A.4.
As for the threading, our Feature-Driven framework yields a very simple solution.
The idea is that applying the
.
This is illustrated in figure A.4.
As for the threading, our Feature-Driven framework yields a very simple solution.
The idea is that applying the
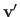 induced warp to
induced warp to
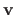 should give
should give
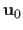 i.e. , the fixed driving features in the texture image.
We thus introduce the reversion operator
i.e. , the fixed driving features in the texture image.
We thus introduce the reversion operator 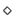 as:
as:
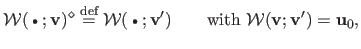 |
(A.12) |
This amounts to solving an exactly determined linear system, the size of which is the number of driving features.
Using equation (A.10), we obtain:
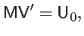 |
(A.13) |
where
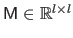 is the matrix defined by
is the matrix defined by
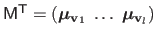 ,
,
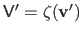 and
and
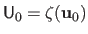 .
The driving features
.
The driving features
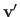 of the reverted warp are thus given by:
of the reverted warp are thus given by:
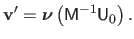 |
(A.14) |
Examples of the reverting process are shown in figure A.5.
We synthesized driving features
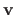 by randomly disturbing a
by randomly disturbing a
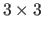 regular grid from its rest position
regular grid from its rest position
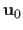 .
The driving features
.
The driving features
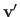 result from reverting the warp
result from reverting the warp
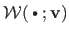 .
Threading warps
.
Threading warps
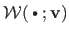 and
and
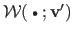 introduce a new set of driving features
introduce a new set of driving features
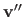 .
As expected, the features
.
As expected, the features
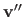 are similar to the original grid
are similar to the original grid
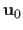 with an average residual error of
with an average residual error of 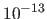 pixels.
pixels.
Figure A.5:
Illustration of the warp reversion process on three examples.
|
 |
Relying on the Feature-Driven parameterization properties, we extend compositional algorithms to non-groupwise warps.
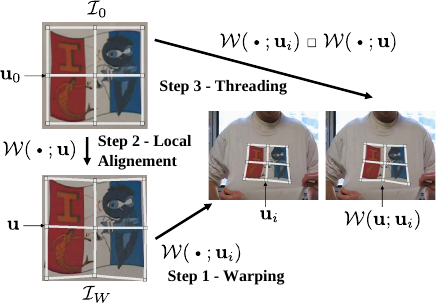
The following three steps are repeated until convergence, as shown in figure A.6:
Note that in previous work (158,75,123) a preliminary step is required before applying the update rule, as reviewed in section A.2.2.
In comparison, our Feature-Driven framework makes it naturally included into the third step.
Illumination changes are handled by globally normalizing the pixel values in the texture and the warped images at each iteration.
Another approach could be used such as the light-invariant approach of (148).
Figure A.6:
The three steps of the Compositional Feature-Driven registration.
|
 |
Contributions to Parametric Image Registration and 3D Surface Reconstruction (Ph.D. dissertation, November 2010) - Florent Brunet
Webpage generated on July 2011
PDF version (11 Mo)
![]() function usually parameterized by a set of
function usually parameterized by a set of ![]() control points
control points
![]() for
for
![]() .
These control points are grouped in a vector
.
These control points are grouped in a vector
![]() where
where
![]() is the matrix defined by
is the matrix defined by
![]() .
We write
.
We write ![]() the warp in its natural parameterization.
The warp
the warp in its natural parameterization.
The warp ![]() is said to be linear when it can be defined as a linear combination of its control points:
is said to be linear when it can be defined as a linear combination of its control points:
![]() and
and
![]() by randomly disturbing a
by randomly disturbing a
![]() regular grid from its rest position
regular grid from its rest position
![]() .
As expected, threading a warp
.
As expected, threading a warp
![]() with the identity
with the identity
![]() returns the original warp i.e.
returns the original warp i.e.
![]() and
and
![]() .
.
![]() by randomly disturbing a
by randomly disturbing a
![]() regular grid from its rest position
regular grid from its rest position
![]() .
The driving features
.
The driving features
![]() result from reverting the warp
result from reverting the warp
![]() .
Threading warps
.
Threading warps
![]() and
and
![]() introduce a new set of driving features
introduce a new set of driving features
![]() .
As expected, the features
.
As expected, the features
![]() are similar to the original grid
are similar to the original grid
![]() with an average residual error of
with an average residual error of ![]() pixels.
pixels.